by the numbers

alpha project team members

T Jean Egan
Rebecca Bell

Prime Numbers

Q1: 1 is a prime number. TRUE or FALSE?

Q2: what part of the formal definition of a prime number precludes 1?

Q3: "integers greater than 1" and "natural numbers other than 1" refer to the same set of numbers. TRUE or FALSE

Q4: since all even numbers are divisible by 2, are there any even prime numbers?

Q5: TRUE or FALSE change "greater than" to "other than" in the phrase "integers greater than 1" for the same set.

Ian Steward:

     Who would have imagined that something as straightforward as the natural numbers (1, 2, 3, 4, . . .) could give birth to anything so baffling as the prime numbers (2, 3 ,5, 7, 11, . . .)?

in Jumping Champions, Scientific American, (2000)

thoughts from the author:

Prime numbers. Beautiful, mysterious, deceptively simple, and yet tantalizing in the depth of their complexity. If we listen closely when mathematicians talk of primes, listen beyond their rigorous definitions, their theorems, the equations of their proofs, we hear a captivating story infused with awe and wonder.

Prime numbers are the numbers on which, it is said, all other natural numbers are built. The prerequisite for inclusion is straight forward: a natural number other than 1, evenly divisible only by 1 and itself. 2, 3, 5, 7, 9, 11, 13, 17, 19, and so on. Simple, yes?

Then again, perhaps not.

The problem, to state it simply: once we have found one, say the largest one we know of, we don't quite know where we will find the next one. We know it's out there but is it the next counting number, or the one after that, or after that? We can't quite say with any certainty where it might be. And therein lies the cruxt of the problem. We are unable to pinpoint the distribution of primes within the natural numbers.

It is exactly this juxtaposition of simplicity and complexity that forever fascinates.

So here we begin our twitter quiz (#numberquiz). And what better place to begin, than at the beginning, with the basic definitions.

Enjoy . . .
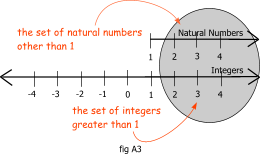
T Jean Egan

answers:

A1: FALSE. Although the primality of 1 has come and gone over the years, we now accept, by definition, that 1 is not a prime number. Neither is it a composite number. It is a special case in the natural numbers defined as unit.

A2: The exact phrase will depend on the source of the definition you use i.e. the math text or math book from which you are quoting. Most commonly, the phrase will be either "integers greater than 1" or "natural numbers other than 1". Both exclude 1 from the set of numbers under consideration.

A3: TRUE. The resulting sets are the same as in fig A3.

A4: Yes, 2 itself.

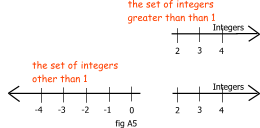
A5: FALSE. For the case of "integers greater than 1", one, zero, and all negatives are removed leaving only the counting numbers 2, 3, 4, and so on, left in the set. For the case of "integers other than 1, only 1 is removed leaving all the negative integers, zero, and all the counting numbers 2, 3, 4, and so on as shown in fig A5.

Leonard Euler:

     Mathematicians have tried in vain to this day to discover some order in the sequence of prime numbers, and we have reason to believe that it is a mystery into which the mind will never penetrate.

in G. Simmons, Calculus Gems, McGraw-Hill, New York, 1992

and more . . .

John Voight Seeks Prime Secrets

In this engaging article by Joshua E. Brown, John Voight, Professor of Mathematics and Computer Science at Vermont University, discusses prime numbers and how classical problems apply to modern cryptography and online security.

The Prime Pages

A comprehensive prime number resource with everything from clearly stated concepts and explanations, prime number history, and theorems, to prime number lists, and even some suggestions as to where to start your studies should you want to delve deeper into primes and number theory. Created and maintained by Dr. K. Caldwell, Department of Mathematics and Statistics, at the University of Tennesse at Martin, this is a great place to start your prime number investigation.

The Electronic Frontier Foundation's Cooperative Computing Award

Sponsored by the Electronic Frontier Foundation (EFF), the search is on for the largest prime of at least 100,000,000 decimal digits. With a cash award of $150,000, finding primes can be lucrative business for your and a few of your closest friends. The GIMPS network, thousands strong, in conjunction with the UCLA Mathematics Department took the last award claiming both worldwide acclaim along with $100,000.